Menjelajahi Dunia Tiga Dimensi: Soal-Soal Menarik Bangun Ruang untuk Kelas 4 SD

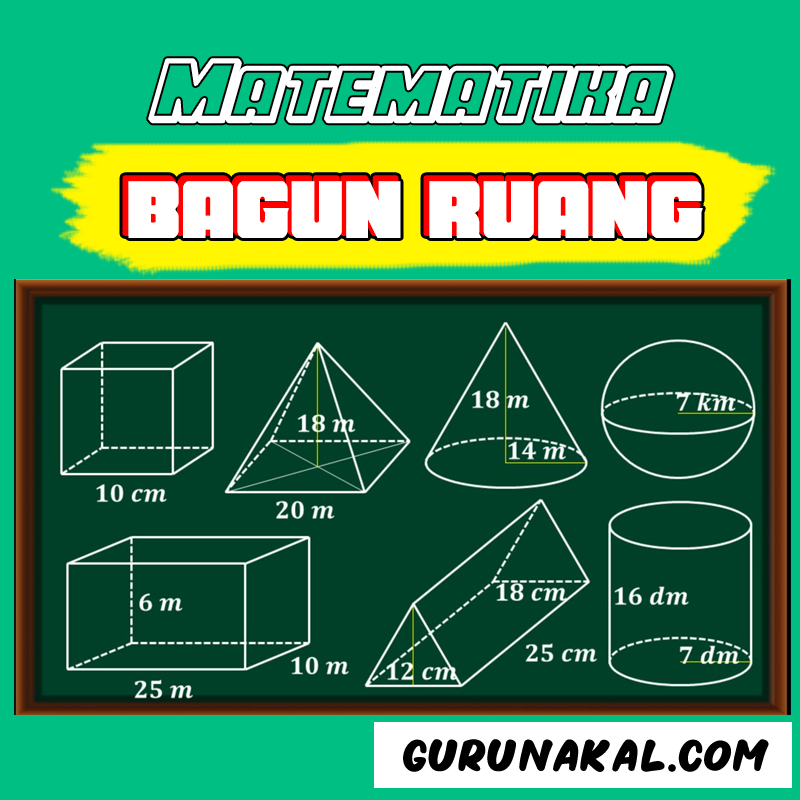
Dunia di sekitar kita dipenuhi dengan berbagai bentuk. Mulai dari bola yang kita gunakan untuk bermain, kotak pensil yang menampung alat tulis kita, hingga rumah tempat kita tinggal, semuanya adalah contoh bangun ruang. Bagi siswa kelas 4 Sekolah Dasar, memahami konsep bangun ruang adalah langkah penting dalam mengembangkan pemahaman spasial dan kemampuan memecahkan masalah.

Dalam artikel ini, kita akan menyelami lebih dalam dunia bangun ruang yang seringkali menjadi topik menarik sekaligus menantang bagi anak-anak. Kita akan membahas beberapa bangun ruang dasar yang umum dipelajari di kelas 4, mulai dari ciri-cirinya, hingga berbagai macam soal latihan yang akan membantu memperkuat pemahaman mereka. Mari kita bersiap untuk menjelajahi dunia tiga dimensi ini bersama-sama!

Apa Itu Bangun Ruang?

Sebelum kita masuk ke soal-soal, penting untuk diingat kembali apa itu bangun ruang. Bangun ruang adalah bangun tiga dimensi yang memiliki ruang, volume, dan luas permukaan. Berbeda dengan bangun datar yang hanya memiliki panjang dan lebar (dua dimensi), bangun ruang memiliki tambahan dimensi yaitu tinggi.

Bangun ruang memiliki elemen-elemen penting yang perlu kita kenal:

• Sisi: Permukaan datar yang membentuk bangun ruang.
• Rusuk: Garis pertemuan antara dua sisi bangun ruang.
• Titik Sudut: Pertemuan antara tiga rusuk atau lebih.

Bangun Ruang Populer di Kelas 4 SD

Di jenjang kelas 4 SD, biasanya siswa diperkenalkan pada beberapa bangun ruang dasar yang memiliki bentuk dan sifat yang mudah dikenali. Berikut adalah beberapa yang paling umum:

1. Kubus: Bayangkan sebuah dadu. Itulah kubus!

   • Ciri-ciri: Memiliki 6 sisi yang semuanya berbentuk persegi dan berukuran sama. Memiliki 12 rusuk yang sama panjang dan 8 titik sudut.
   • Contoh: Dadu, kotak kado berbentuk sempurna, beberapa jenis balok es.

2. Balok: Mirip dengan kubus, tetapi sisi-sisinya bisa berbentuk persegi panjang dengan ukuran yang berbeda.

   • Ciri-ciri: Memiliki 6 sisi yang semuanya berbentuk persegi panjang. Sisi-sisi yang berhadapan memiliki ukuran dan bentuk yang sama. Memiliki 12 rusuk dan 8 titik sudut.
   • Contoh: Kotak sepatu, buku, kulkas, batu bata.

3. Prisma Segitiga: Bangun ruang yang memiliki alas dan tutup berbentuk segitiga, serta sisi tegak berbentuk persegi panjang.

   • Ciri-ciri: Memiliki 5 sisi (2 sisi segitiga sebagai alas dan tutup, serta 3 sisi persegi panjang sebagai sisi tegak). Memiliki 9 rusuk dan 6 titik sudut.
   • Contoh: Tenda pramuka (beberapa model), potongan keju berbentuk segitiga.

4. Tabung: Bayangkan kaleng minuman atau pipa.

   • Ciri-ciri: Memiliki 2 sisi datar berbentuk lingkaran (alas dan tutup) serta 1 sisi lengkung yang menyelimuti. Tidak memiliki rusuk dan titik sudut yang tajam seperti kubus atau balok.
   • Contoh: Kaleng susu, gelas, pipa, lilin.

5. Kerucut: Seperti topi ulang tahun atau corong es krim.

   • Ciri-ciri: Memiliki 1 sisi datar berbentuk lingkaran (alas) dan 1 sisi lengkung yang mengerucut ke satu titik. Memiliki 1 titik puncak.
   • Contoh: Topi ulang tahun, corong, lampu lalu lintas (bagian atas).

6. Bola: Bentuk yang sempurna dan mulus.

   • Ciri-ciri: Hanya memiliki 1 sisi lengkung. Tidak memiliki rusuk maupun titik sudut.
   • Contoh: Bola sepak, bola basket, kelereng.

Mengasah Kemampuan: Soal-Soal Latihan Bangun Ruang Kelas 4

Mari kita uji pemahaman kita dengan berbagai soal yang bervariasi. Soal-soal ini dirancang untuk mencakup konsep-konsep dasar mengenai bangun ruang.

Bagian 1: Identifikasi dan Ciri-ciri Bangun Ruang

1. Bangun ruang yang memiliki enam sisi berbentuk persegi yang semuanya berukuran sama disebut…
   a. Balok
   b. Kubus
   c. Prisma
   d. Kerucut

2. Berapa jumlah rusuk pada bangun ruang balok?
   a. 6
   b. 8
   c. 10
   d. 12

3. Sebuah bangun ruang memiliki alas dan tutup berbentuk segitiga, serta tiga sisi tegak berbentuk persegi panjang. Bangun ruang apakah itu?
   a. Kubus
   b. Tabung
   c. Prisma Segitiga
   d. Limas Segitiga

4. Bangun ruang yang permukaannya hanya terdiri dari satu sisi lengkung adalah…
   a. Tabung
   b. Kerucut
   c. Bola
   d. Limas

5. Bangun ruang yang memiliki satu sisi datar berbentuk lingkaran dan satu titik puncak disebut…
   a. Tabung
   b. Kerucut
   c. Bola
   d. Silinder

6. Sebuah bangun ruang memiliki 12 rusuk dan 8 titik sudut. Bangun ruang tersebut bisa jadi… (pilih dua jawaban yang tepat)
   a. Kubus
   b. Balok
   c. Prisma Segitiga
   d. Tabung

7. Manakah dari benda berikut yang paling menyerupai bangun ruang tabung?
   a. Penggaris
   b. Buku tulis
   c. Kaleng minuman
   d. Kelereng

8. Sebutkan ciri-ciri utama dari bangun ruang kubus!
   …

9. Jelaskan perbedaan mendasar antara kubus dan balok!
   …

10. Sebutkan tiga contoh benda di sekitarmu yang memiliki bentuk seperti bola!
    …

Bagian 2: Menghitung Volume Bangun Ruang

Volume adalah ukuran ruang yang ditempati oleh suatu bangun ruang. Untuk kelas 4, biasanya kita fokus pada bangun ruang yang memiliki rumus volume sederhana.

Rumus Dasar yang Perlu Diingat:

• Volume Kubus: sisi × sisi × sisi (s³)
• Volume Balok: panjang × lebar × tinggi (p × l × t)
• Volume Tabung: Luas alas × tinggi (π × r² × t) – Catatan: Untuk kelas 4, seringkali π dianggap 22/7 atau 3.14, atau soal disederhanakan.
• Volume Prisma Segitiga: Luas alas segitiga × tinggi prisma (½ × alas segitiga × tinggi segitiga × tinggi prisma)

11. Sebuah kubus memiliki panjang rusuk 5 cm. Berapakah volume kubus tersebut?

12. Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 4 cm. Hitunglah volume balok tersebut!

13. Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Jika π = 22/7, berapakah volume tabung tersebut?

14. Sebuah prisma segitiga memiliki alas segitiga dengan panjang alas 8 cm dan tinggi segitiga 5 cm. Tinggi prisma adalah 12 cm. Berapakah volume prisma segitiga tersebut?

15. Sebuah kotak berbentuk kubus memiliki panjang rusuk 8 cm. Jika kita ingin mengisi kotak tersebut dengan bola-bola kecil berdiameter 2 cm, berapa perkiraan jumlah bola yang bisa masuk? (Soal ini lebih ke pemahaman konsep, tidak perlu perhitungan eksak yang rumit).

Bagian 3: Menghitung Luas Permukaan Bangun Ruang

Luas permukaan adalah jumlah luas semua sisi yang membentuk bangun ruang.

Rumus Dasar yang Perlu Diingat:

• Luas Permukaan Kubus: 6 × sisi × sisi (6s²)
• Luas Permukaan Balok: 2 × (pl + pt + lt)
• Luas Permukaan Tabung: Luas alas + Luas tutup + Luas selimut (2πr² + 2πrt) – Seringkali disederhanakan untuk kelas 4.
• Luas Permukaan Prisma Segitiga: 2 × Luas alas segitiga + Keliling alas segitiga × tinggi prisma

16. Hitunglah luas permukaan sebuah kubus yang memiliki panjang rusuk 7 cm!

17. Sebuah balok memiliki panjang 15 cm, lebar 8 cm, dan tinggi 5 cm. Hitunglah luas permukaannya!

18. Sebuah tabung memiliki jari-jari alas 5 cm dan tinggi 10 cm. Jika π = 3.14, berapakah luas permukaan tabung tersebut? (Hitung luas alas, luas tutup, dan luas selimut secara terpisah lalu jumlahkan).

19. Sebuah prisma segitiga memiliki alas segitiga sama sisi dengan panjang sisi 6 cm. Tinggi prisma adalah 10 cm. Hitunglah luas permukaannya! (Perlu mencari luas segitiga sama sisi dan kelilingnya).

20. Sebuah kotak sepatu berbentuk balok akan dilapisi kertas kado. Jika panjang kotak 30 cm, lebar 20 cm, dan tinggi 15 cm, berapa luas kertas kado minimal yang dibutuhkan untuk menutupi seluruh permukaan kotak?

Kunci Jawaban dan Pembahasan

Mari kita periksa jawaban Anda dan pahami cara mengerjakannya!

Bagian 1: Identifikasi dan Ciri-ciri Bangun Ruang

1. Jawaban: b. Kubus
   Pembahasan: Kubus memiliki enam sisi yang semuanya berbentuk persegi dan berukuran sama.

2. Jawaban: d. 12
   Pembahasan: Balok memiliki 12 rusuk. Bayangkan rusuk-rusuk pada bagian alas, bagian atas, dan rusuk-rusuk tegak yang menghubungkan alas dan atas.

3. Jawaban: c. Prisma Segitiga
   Pembahasan: Ciri-ciri ini sesuai dengan definisi prisma segitiga.

4. Jawaban: c. Bola
   Pembahasan: Bola adalah satu-satunya bangun ruang yang permukaannya sepenuhnya melengkung.

5. Jawaban: b. Kerucut
   Pembahasan: Kerucut memiliki alas lingkaran dan mengerucut ke satu titik puncak.

6. Jawaban: a. Kubus, b. Balok
   Pembahasan: Kubus dan balok sama-sama memiliki 12 rusuk dan 8 titik sudut.

7. Jawaban: c. Kaleng minuman
   Pembahasan: Kaleng minuman memiliki bentuk silinder yang merupakan ciri khas tabung.

8. Jawaban: Kubus memiliki 6 sisi yang semuanya berbentuk persegi dan berukuran sama. Kubus memiliki 12 rusuk yang sama panjang. Kubus memiliki 8 titik sudut.

9. Jawaban: Perbedaan mendasar adalah pada bentuk sisi-sisinya. Kubus memiliki semua sisi berbentuk persegi yang ukurannya sama. Balok memiliki sisi-sisi berbentuk persegi panjang, di mana sisi-sisi yang berhadapan memiliki ukuran dan bentuk yang sama, tetapi sisi-sisi yang berdekatan bisa memiliki ukuran yang berbeda.

10. Jawaban: Contohnya adalah bola sepak, bola basket, kelereng, bola bekel, globe, jeruk.

Bagian 2: Menghitung Volume Bangun Ruang

11. Jawaban: Volume = 5 cm × 5 cm × 5 cm = 125 cm³
    Pembahasan: Menggunakan rumus volume kubus s³.

12. Jawaban: Volume = 10 cm × 6 cm × 4 cm = 240 cm³
    Pembahasan: Menggunakan rumus volume balok p × l × t.

13. Jawaban: Luas alas = π × r² = 22/7 × 7 cm × 7 cm = 22 × 7 cm² = 154 cm². Volume = Luas alas × tinggi = 154 cm² × 10 cm = 1540 cm³.
    Pembahasan: Pertama hitung luas alas lingkaran, lalu kalikan dengan tinggi tabung.

14. Jawaban: Luas alas segitiga = ½ × alas segitiga × tinggi segitiga = ½ × 8 cm × 5 cm = 20 cm². Volume = Luas alas segitiga × tinggi prisma = 20 cm² × 12 cm = 240 cm³.
    Pembahasan: Hitung luas alas segitiga, lalu kalikan dengan tinggi prisma.

15. Jawaban: Perkiraan jumlah bola yang bisa masuk adalah cukup banyak, mungkin ratusan, tergantung bagaimana bola-bola itu tersusun. Soal ini menekankan pemahaman bahwa volume benda padat (bola) mengisi ruang dalam bangun ruang (kotak). Perhitungan eksaknya memerlukan konsep yang lebih lanjut.

Bagian 3: Menghitung Luas Permukaan Bangun Ruang

16. Jawaban: Luas permukaan = 6 × sisi × sisi = 6 × 7 cm × 7 cm = 6 × 49 cm² = 294 cm².
    Pembahasan: Menggunakan rumus luas permukaan kubus 6s².

17. Jawaban: Luas permukaan = 2 × (pl + pt + lt) = 2 × ((15 cm × 8 cm) + (15 cm × 5 cm) + (8 cm × 5 cm)) = 2 × (120 cm² + 75 cm² + 40 cm²) = 2 × 235 cm² = 470 cm².
    Pembahasan: Menggunakan rumus luas permukaan balok.

18. Jawaban:

    • Luas alas = πr² = 3.14 × (5 cm)² = 3.14 × 25 cm² = 78.5 cm².
    • Luas tutup = Luas alas = 78.5 cm².
    • Luas selimut = 2πrt = 2 × 3.14 × 5 cm × 10 cm = 6.28 × 50 cm² = 314 cm².
    • Luas permukaan total = Luas alas + Luas tutup + Luas selimut = 78.5 cm² + 78.5 cm² + 314 cm² = 471 cm².
      Pembahasan: Menghitung setiap bagian permukaan tabung lalu menjumlahkannya.

19. Jawaban:

    • Luas alas segitiga sama sisi (s=6 cm): Luas = (s²√3)/4 = (6²√3)/4 = (36√3)/4 = 9√3 cm² (Jika tidak diajarkan rumus ini, bisa dicari dengan tinggi segitiga: tinggi = √(6² – 3²) = √27 = 3√3 cm. Luas = ½ × 6 × 3√3 = 9√3 cm²).
    • Keliling alas segitiga = 6 cm + 6 cm + 6 cm = 18 cm.
    • Luas selimut prisma = Keliling alas × tinggi prisma = 18 cm × 10 cm = 180 cm².
    • Luas permukaan prisma = 2 × Luas alas + Luas selimut = 2 × 9√3 cm² + 180 cm² = 18√3 cm² + 180 cm². (Jika menggunakan pendekatan yang lebih sederhana tanpa √3, maka nilai √3 sekitar 1.732, sehingga 9√3 ≈ 15.59 cm², luas permukaan ≈ 2 15.59 + 180 ≈ 31.18 + 180 ≈ 211.18 cm²). Catatan: Untuk kelas 4, soal prisma segitiga biasanya menggunakan alas segitiga siku-siku atau diketahui tingginya agar perhitungan lebih mudah.*
      Pembahasan: Soal ini sedikit lebih kompleks karena melibatkan segitiga sama sisi. Pendekatan yang lebih umum di kelas 4 adalah menggunakan alas segitiga siku-siku.

20. Jawaban: Luas kertas kado minimal = Luas permukaan balok = 470 cm².
    Pembahasan: Sama seperti soal nomor 17, kita menghitung luas permukaan balok.

Penutup

Memahami bangun ruang adalah keterampilan fundamental yang akan terus digunakan siswa di jenjang pendidikan selanjutnya dan bahkan dalam kehidupan sehari-hari. Melalui latihan soal yang bervariasi, siswa dapat mengasah kemampuan identifikasi, visualisasi, dan perhitungan mereka. Ingatlah bahwa kesabaran dan latihan adalah kunci utama dalam menguasai materi ini.

Teruslah berlatih, jangan ragu untuk bertanya, dan nikmati petualangan Anda dalam menjelajahi dunia tiga dimensi yang menakjubkan!